2025年12月11日に「グラフィカルモデルと因果探索 with R」という書籍を出版します。機械学習の数理100問シリーズの5作目です。阪大に着任する前から、30年以上かけて手掛けてきた分野で、集大成というべき内容です。グラフィカルモデル、カーネル、PCアルゴリズム、LiNGAMについて正確に記述しました。多くの方にお読みいただけるよう、難しいトピックは避け、やさしく書きました。

下記がまえがきからの抜粋です。
グラフィカルモデルは、複雑な確率変数間の関係を視覚的かつ数理的に捉えることができる、非常に魅力的な枠組みです。確率論とグラフ理論を融合することで、ベイズネットワークやマルコフネットワークといった、実世界の構造をモデル化する手法が体系化されてきました。こうしたモデルを用いれば、単なる相関の把握にとどまらず、変数間の因果的な構造を明らかにする「因果探索」へと進むことが可能になります。
本書で取り上げる因果探索は、変数間の依存関係(いわゆる骨格)を推定するだけでなく、その上に矢印を付けて、変数の因果的な順序を特定するという、2つの重要なステップから成り立っています。この問題は、統計学の従来の枠組みだけでは十分に扱えないものでしたが、近年では、カーネル法、非ガウス性の活用、情報量基準、さらにはベイズ的な周辺尤度といった先端的な技術によって、より柔軟かつ理論的にも整合的なアプローチが可能になってきています。
グラフィカルモデルの魅力は、数式やコードだけでは得がたい「構造の直感」を私たちにもたらしてくれる点にあります。図として描ける、言葉で説明できる、手で動かして理解できる——このような視覚的かつ操作的な理解は、抽象的な確率論や統計モデリングの世界を、ぐっと身近なものにしてくれます。統計と機械学習の狭間に立ち、理論と実践の橋渡しをするこの分野は、今後ますます重要な役割を果たしていくと確信しています。
私がグラフィカルモデルと出会ったのは、まだ「機械学習」という言葉が今ほど一般的ではなかった1990年代前半のことでした。当時、早稲田大学で助手をしていた私は、理工学部の近くにあった明治通り沿いの洋書専門書店で、たまたま国際会議UAI(Uncertainty in Artificial Intelligence)のプロシーディングを手に取る機会がありました。そこには、ベイズネットワークの構造をどのようにデータから学習するかについての、非常に洗練された議論が展開されており、一気に引き込まれました。
その頃ちょうど、Jorma Rissanen先生が提唱されたMDL(最小記述長)原理にも出会い、「データの背後にあるシンプルな構造を見出す」という考え方に深く共感しました。私はすぐに、サンプルからグラフ構造を推定する問題にMDLを適用し、1993年のUAI会議でその成果を発表することができました。これは、日本人としてグラフィカルモデルの構造学習を国際的に紹介した最初期のひとつであると聞いております。
それ以来、私はグラフィカルモデルの可能性に魅せられ、研究を続けてきました。ひと目では簡単そうに見える図の背後には、膨大な数理的課題が横たわっています。それら一つひとつと向き合い、丁寧に解きほぐしていく過程は、研究者としての私の原点であり、また今日までの歩みの核でもあります。
本書で扱う因果探索は、依存関係の探索と、変数順序の探索という、2つの重要な課題を扱います。
\begin{boxnote}
\centering
因果探索 = 依存関係の探索 +変数順序の探索
\end{boxnote}
与えられた$p$個の変数と$n$個のサンプルに対して、どちらか一方だけでは正しい因果構造を描くことはできません。データをツールに放り込めば、依存関係や順序らしきものは簡単に出てきます。しかし、期待と違う結果や直感に反する結果が出たとき、なぜそのような結果になったのか、アルゴリズムの動作を説明できなければ、単なる結果にとどまってしまいます。論文にまとめることもできず、上司やクライアントに納得してもらうことも難しいでしょう。
今回の書籍は、グラフィカルモデルにおける因果探索にテーマを絞り、カーネル法やベイズ的アプローチといった現代的な技術も取り入れています。また、清水昌平先生(大阪大学)の考案された、変数順序の探索で有向なLiNGAMに関しては、その本質を記述するように心がけました。
さらに、2019年に大学院講義で使用した演習問題や、過去10回以上実施してきたオンライン少人数セミナーの教材もふんだんに活用しています。これまでに出版してきた「機械学習の数理100問シリーズ」と同様に、ただ手順を覚えるだけでなく、「なぜそうなるのか」を考え抜き、心から感動していただける本を目指しました。
このように、本書の構成は、理論と実装、直感と厳密性のバランスをとりながら段階的に理解を深められるように設計されています。以下の図は各章の関係性と位置づけを視覚的に示したものです。
本書は、グラフィカルモデル全体を網羅するのではなく、因果探索に的を絞って理論と実践を深く掘り下げた専門書です。特に以下の点で、他書には見られない独自性を有しています:
1. ベイズネットワーク全体を扱うのではなく、因果探索に関する理論と手法に特化しています。中でも、LiNGAMやスコアベースの構造学習については、理論から実装まで踏み込み、詳細に解説しています。
2. カーネル法による統計的検定(HSIC, KCIなど)について、PCアルゴリズムやLiNGAMへの応用を見据え、その数理的本質を簡潔かつ直感的に記述しています。
3. 構造学習におけるベイズ的アプローチとして、周辺尤度と情報量基準(とくにBIC)との関係を定式化し、背景理論を丁寧に掘り下げています。BDeuやJeffreys事前分布の含意や限界についても明快に示しています。
4. 単なる概念紹介にとどまらず、RやPythonによる実装コードを可能な限り掲載し、再現可能な形で理解が進むよう配慮しています。
5. 初学者にも配慮し、重要なアイデアは図解や例を通して直感的に説明しています。高度な内容も、視覚的な補助と段階的な構成により、理解しやすく工夫されています。
本書の主眼はあくまで実践的な因果探索の理解ですが、理論的背景をより深く掘り下げたい読者のために、付録では次のような高度な定理や導出も取り上げました。
1. Darmois–Skitovitch定理
2. Murphyによる周辺尤度の導出(正規平均・逆Wishart事前)
3. Verma–Pearlの構造学習に関する基本定理
これらは、因果探索の数理的理解をさらに深めたい読者に向けた内容であり、本書の主たる内容を読み進めるうえで必須ではありません。数式に不安のある方は読み飛ばしていただいて問題ありませんし、興味をもった読者には、理論の背景を納得のいく形で確認できる読み応えある補足となるでしょう。
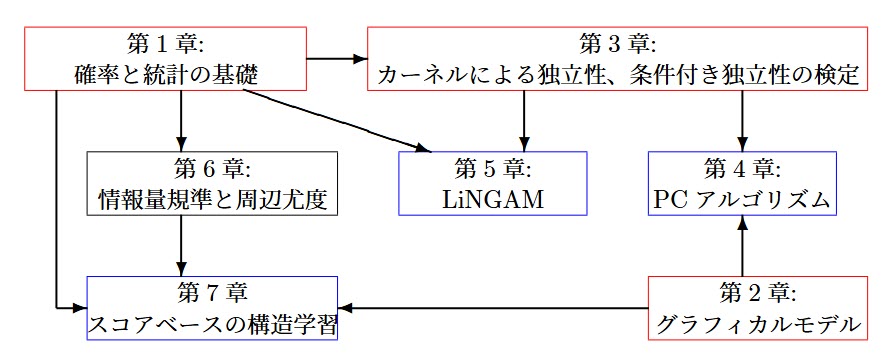
各章の流れを下の図のようにまとめました。
第1章では、本書の後半で展開される因果探索手法の理解に必要な確率・統計の基礎を確認します。
第2章では、グラフィカルモデルにおける条件付き独立性や分離性など、最小限の概念を学びます。
第3章では、カーネル法による独立性・条件付き独立性の検定(HSIC, KCIなど)を扱います。
第4章では、この検定を用いたPCアルゴリズムを紹介します。これは、条件付き独立性の検定を通じて、変数間の依存構造(骨格)を特定する制約ベースの構造学習手法です。
第5章では、非ガウス性に基づいて因果順序を推定するLiNGAMを扱い、DirectLiNGAMアルゴリズムでは第3章の独立性検定が重要な役割を担います。
第6章では、スコアベースの構造学習に必要な理論的背景として、情報量基準(AIC, BIC)や周辺尤度の定式化と性質を扱います。
第7章では、それを活用したスコアベースの構造学習手法を紹介します。これはPCアルゴリズムと同様に変数構造を推定しますが、スコア評価に基づいて候補構造を比較し、最適なモデルを選択するというアプローチをとります。
図中の赤い枠は基礎理論を扱う章、青い枠は因果探索の具体的手法を扱う章を示しています。
本書は、因果探索という難題に真正面から取り組むと同時に、グラフィカルモデルがもつ「知的な美しさ」と「応用としての力強さ」の両面を、学生、実務家、そして研究者の皆さまにお伝えすることを目指しています。本書を手に取ってくださった皆様が、因果探索の奥深い世界への理解を一層深めてくださることを、心より願っています。