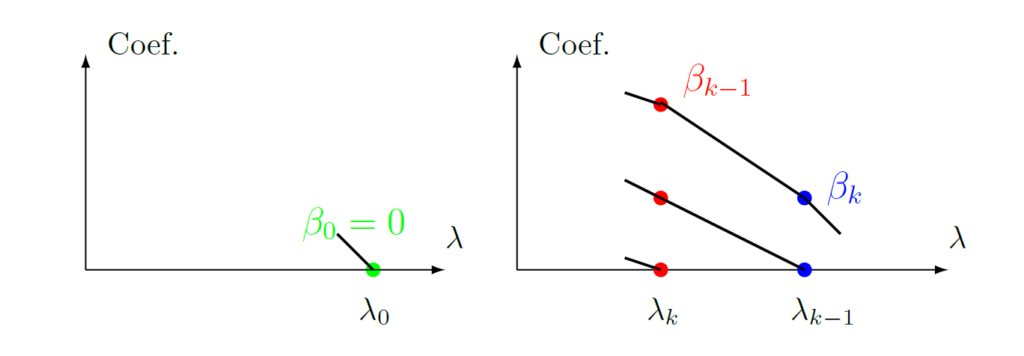
Lasso では、非ゼロ係数が1個以上ある$\lambda$で最大の値が一意に決まります。2乗誤差を$N$で割らない場合、そのような$\lambda$ は$\langle x^{(j)}, y\rangle$の絶対値の最大値($1\leq j\leq p$)になります。ただし、$x^{(j)}$は$X\in {\mathbb R}^{N\times p}$の$j$列目、$y\in {\mathbb R}^N$であるとします。そのような$\lambda$, $j$を今後$\lambda_0$, $j_0$と書きます。

LARSは、$\lambda\leq \lambda_0$に対して、$\beta(\lambda)$を以下のように定義します: それまでに$\lambda_0,\lambda_1,\ldots,\lambda_{k-1}$, $\beta_0=0,\beta_1,\ldots,\beta_{k-1}$, ${\cal S}=\{j_0,\ldots,j_{k-1}\}$が得られているとして($k\geq 1$)、以下を繰り返します。

1. 最初の$k$成分がゼロ、残り$p-k$成分が0のベクトル$\Delta_{k-1}$を定義
2. $\lambda\leq \lambda_{k-1}$について、 $\beta(\lambda):=\beta_{k-1}+(\lambda_{k-1}-\lambda)\Delta_{k-1}$および$r(\lambda):=y-X\beta(\lambda)$を定義。
3. $\langle x^{(j_k)},r(\lambda_k)\rangle$の絶対値が$\lambda_k$に一致する 最大の$\lambda_k$およびその$j_k$を見出し、$j_k$を$\cal S$に加える。
4. $\beta(\lambda)$, $r(\lambda)$の定義域を$\lambda_k\leq \lambda$に限定し、$\beta_k:=\beta(\lambda_k)$とおく。

ここで、$$\Delta_{k-1}:=\left[
\begin{array}{c}
(X_{\cal S}^TX_{\cal S})^{-1}X_{\cal S}^Tr(\lambda_{k-1})/\lambda_{k-1}\\
0
\end{array}
\right]\ ,
$$
と選べば、各$k=0,1,\ldots,p-1$について、$$\lambda\leq \lambda_k\Longrightarrow \langle x^{(j_k)}, r(\lambda)\rangle=\lambda$$
が成立します。ただし、$X_{\cal S}\in {\mathbb R}^{N\times k}$は、$x^{(j)}$, $j\in {\cal S}$を列に持つ$X$の部分行列とします。